V elektrotechnice běžně používané potenciometry se podle závislosti průběhu změny hodnoty odporové vrstvy na poloze jezdce dělí do dvou kategorií: lineární a logaritmické. (Jsou i exponenciální, ale ty nepatří mezi běžně používané.) Dodatečným připojením pevných odporů (rezistorů) ke dvěma větvím tvořeným body začátek–jezdec resp. jezdec–konec lze charakter průběhu dělicího poměru potenciometru dále upravit.
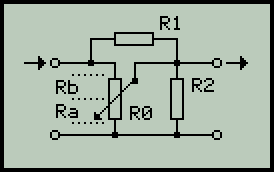
Na zobrazeném schematu jsou důležité především použité symboly. Že R0 udává hodnotu potenciometru a R1, R2 jsou hodnoty připojovaných rezistorů, je zcela evidentní. Symboly Ra a Rb reprezentují odpor obou sekcí potenciometru: začátek–jezdec a jezdec–konec. Všechna označení respektují komentáře obsažené ve zdrojových textech, zejména v podprogramu CALCVAL.
Následující text se zabývá výpočtem a zobrazením dělicího poměru pro oba typy potenciometrů (s lineárním a logaritmickým průběhem) na HP-50g.
Výpočet průběhu | ↑ ↓ |
Prvním krokem k úspěchu je stanovení funkce převodu poloha_jezdce → dělicí_poměr potenciometru s rozsahem vstupní a výsledné hodnoty. Obě proměnné - nezávislá x (poloha jezdce) i závislá y (dělicí poměr) - jsou v intervalu 0 až 1. Pokud má průběh být lineární, je to snadné, nic se nepočítá:
y = x
V případě logaritmického průběhu zadaným podmínkám vyhoví funkce:
y = a·log(b·x+1)
Koeficienty a a b vycházejí ze zadaného útlumu v celém rozsahu děliče určeného hodnotou g v [dB].
b = 10 g/20−1
a = 20/g
Zdrojové texty | ↑ ↓ |
Objekty, z nichž je celý program složen, lze rozdělit do tří kategorií:
@ @ @ VYPOCET DELICIHO POMERU @ Real CALCVAL(Real xval); « POS2VAL R0 * @ Ra R0 @ R0 Ra OVER @ Ra R0 Ra - @ Rb Ra 'R1' @ 'R1' Rb Ra PARALLEL @ R1b Ra SWAP @ Ra R1b 'R2' @ 'R2' Ra R1b PARALLEL @ R2a R1b DUP @ R2a R2a R1b ROT @ R1b R2a R2a + @ R1b+R2a R2a / @ yval »
{ R0
R1
R2
{ "G[dB]" GdB }
{ }
{ "DRAW" DRAWALL }
{ "HELP" « potlg.gg PICT STO { } PVIEW » }
{ "FONT" « "FONT: "
IF 80 DUP FC?
THEN
SF "Large"
ELSE
CF "Small"
END
+ MSGBOX » }
{ }
{ }
{ "CLEAN" « { COEFA COEFB EQ GdB PPAR POS2VAL R0 R1 R2 TPAR } PURGE » }
{ "DRAW" DRAWALL } }
@ @ @ VSTUPNI BOD VYPOCTU A ZOBRAZENI « @ Event. smazani R0, R1, R2 0. @ znacka {R0 R1 R2 GdB} 1. « IF { 0. 28. } OVER VTYPE POS THEN @ je-li to typ REAL nebo INT... IF DUP RCL 0. > @ ...a je ve spravnem rozsahu... THEN @ ...nebude se mazat DUP RCL I→R SWAP STO END END » DOLIST IF DUP TYPE 0. ≠ @ neni-li to znacka, ale LIST... THEN PURGE @ ...smazat END DROP @ znacka @ Typ potenciometru IF 'GdB' VTYPE 0. < @ neexistuje-li... THEN « » @ ...bude prubeh linearni { COEFB COEFA } PURGE ELSE « COEFB * 1. + LOG COEFA * » GdB 20. / DUP ALOG @ [dB] --> Gain 1. - 'COEFB' STO INV 'COEFA' STO END 'POS2VAL' STO @ Event. nastaveni R0 IF 'R0' VTYPE 0. < @ neexistuje-li... THEN 1. 'R0' STO @ ...nastavit na 1. END @ Spolecne hodnoty PPAR A TPAR (0., 0.) (1., 1.) PDIM {0. .05 0. 2. 0. TAB} 'TPAR' STO @ Smazat predchozi a vykreslit osy ERASE {0.1 0.2} ATICK DRAX @ Prubeh bez R1, R2 RCLF @ uschovat FLAGS # 5 RES @ vykreslovat jen kazdy 5. pixel -31 SF @ nespojovat krivku 'POS2VAL(X)' STEQ DRAW @ Prubeh s R1, R2 0. RES @ vykreslovat vse... -31 CF @ ...a spojite 'CALCVAL(X)' STEQ DRAW STOF @ obnovit FLAGS @ Hodnoty odporu {R0 R1 R2} 1. « IF DUP VTYPE 0. ≥ @ existuje-li promenna THEN DUP @ 'R1' 'R1' →STR 2. OVER SIZE 1. - SUB "=" + SWAP @ 'R1' "R1=" RCL @ 470. "R1=" ←trim EVAL @ 470 "R1=" →STR @ "470" "R1=" + @ "R1=470" ←v2g EVAL ELSE DROP END » 78. @ ←ypos @ @ @ Prevod text.retezce na GROB a pridani do PICT @ void ←v2g(String text); « 80 FC? @ 0.|1. "R0=470." DUP @ 0.|1. 0.|1. "R0=470." NOT @ 1.|0. 0.|1. "R0=470." DUP @ 1.|0. 1.|0. 0.|1. "R0=470." + @ 2.|0. 0.|1. "R0=470." 8. @ 8. 2.|0. 0.|1. "R0=470." + @ 10.|8. 0.|1. "R0=470." '←ypos' SWAP @ 10.|8. '←ypos' 0.|1. "R0=470." STO- @ 0.|1. "R0=470." →GROB @ grob PICT @ pict grob OVER SIZE DROP @ #width pict grob NEG #131d + @ #xpos pict grob ←ypos R→B 2. @ 2. #ypos #xpos pict grob →LIST @ {#x #y} pict grob ROT @ grob {#x #y} pict GOR » @ @ @ Eventualni odstraneni koncoveho znaku '.' @ Integer ←trim(Real); « IFERR R→I THEN END » → ←ypos ←v2g ←trim « DOLIST IF 'GdB' VTYPE 0. ≥ THEN @ je to logaritmicky prubeh "G=" GdB @ 50. "G=" ←trim EVAL @ 50 "G=" →STR @ "50" "G=" + "dB" + @ "G=50dB" ←v2g EVAL END » @ Pockat na klavesu 0 IFERR WAIT THEN END DROP »
@ @ @ PARALELNI ZAPOJENI REZISTORU @ Real PARALLEL(Alg rname, Real v2); « @ rname v2 → rname « @ v2 IF rname VTYPE 0. ≥ THEN @ v2 rname @ 'rname v2 RCL @ v1 v2 DUP2 @ v1 v2 v1 v2 * @ v1*v2 v1 v2 UNROT @ v1 v2 v1*v2 + @ v1+v2 v1*v2 / @ result END » »
Použití programu | ↑ ↓ |
Dobrým začátkem je aktivace obsahu proměnné CST stiskem klávesy CUSTOM. Soft MENU obsahuje ve směru zleva doprava Soft KEYs pro přístup k hodnotám rezistorů R0 (F1), R1 (F2) a R2 (F3). Další v pořadí je hodnota útlumu děliče G[dB] (F4). (Přístup k hodnotám rezistorů a útlumu použitím Soft KEYs je totožný s přístupem k proměnným po stisku VAR.) Zcela vpravo je DRAW (F6) - spuštění výpočtu s vykreslením grafu. Soft MENU pokračuje po stisku NXT dalšími položkami. První vlevo je HELP (F1), po jejímž stisku je zobrazeno schema pro možnost rekapitulace pozic a označení součástek v zapojení. Následuje přepínač velikosti písma popisků hodnot v grafech FONT (F2). Předposlední je CLEAN (F5). Touto volbou jsou smazány všechny proměnné, které program svou činností vytvoří, nebo pro svou činnost vyžaduje. Stejně jako první stránka Soft MENU i ta druhá končí položkou DRAW (F6).
Pokud bude po nainstalování prvním stiskem DRAW (F6), na displeji kalkulátoru bude k vidění graf s (již zmíněnou) funkcí y = x, tj. přímka jdoucí z bodu (0,0) do bodu (1,1), no prostě čára z levého dolního do pravého horního rohu displeje. Nic, co by stálo za řeč. Zajímavé je snad jen implicitní přiřazení R0=1. Situace se nijak zvlášť nezlepší ani po zadání hodnoty potenciometru R0=470 (třeba sekvencí stisků kláves 4 7 0 L-Shift R0 (F1)). — Něco se začne dít připojením některého z pevných rezistorů po zadání jeho hodnoty. Např. R1=180. — Ještě "hezčí" obrázek zařídí nastavení R2=220. — Pro vyčerpání všech možností zbývá vyřadit rezistor R1: ∞ L-Shift R1 (F2)).
Dodatky a vysvětlivky
K přepnutí do logaritmického módu dojde zápisem platné hodnoty do proměnné GdB zastoupené klávesou G[dB] (F4). Než k tomu dojde, hodí se začít s čistým stolem. To zajistí stisk CLEAN (F5). Je v druhé stránce Soft MENU, možná to bude chtít stisknout NXT. Za vyzkoušení stojí i přepnutí velikosti písma - stačí stisknout FONT (F2) a zobrazí se dialog informující o aktuálním nastavení.
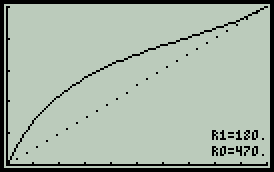
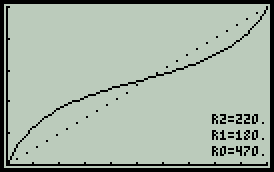
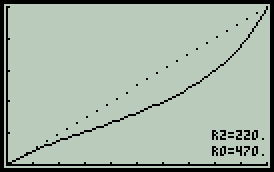
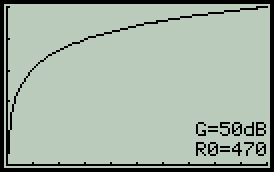
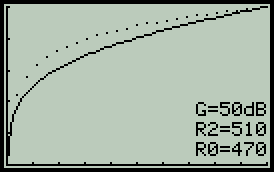
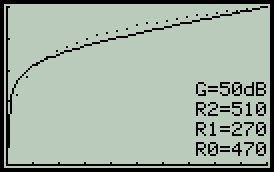
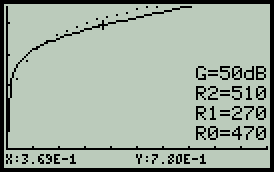
Předmětem zájmu klidně může být potenciometr stejné hodnoty jako v předchozím případě, tedy R0=470. Útlum děliče bude běžně používaných 50dB, GdB=50. — Výsledek na prvním obrázku ukazuje pouze vlastní průběh potenciometru - tečkovaná křivka (výchozí neovlivněný průběh) splývá s plnou. Je také patrné odlišení popiskem G=50dB, které u lineárního módu pochopitelně chybí. — Aby zde prováděné experimenty trochu připomínaly realitu, potenciometr bude zatížen impedancí R2=510. Co to s ideálním průběhem udělá je vidět na prostředním grafu. — Ke vzniklému problému je třeba zaujmout stanovisko a přijmout příslušné opatření, nejlépe připojením kompenzačního rezistoru R1=270. Není to ideální, ale poslední z trojice obrázků je důkazem mírného zlepšení.
Poněkud nedomyšleně působí popisky hodnot v grafech. Zatímco hodnoty potenciometru a dodatečně připojovaných pevných rezistorů R0, R1, R2 nejsou doplněny fyzikální jednotkou, v případě útlumu tato nechybí (viz G=50dB). Moc pěkné to není, ale zdůvodnit se to dá. Hodnoty odporů v praxi mohou být v řádu jednotek (u potencimetru spíše stovek), tisíců nebo miliónů ohmů, např. 100Ω, 10kΩ, 1MΩ. V předchozích ukázkách - stejně jako v praxi - se předpokládá, že hodnoty použitých součástek budou přibližně stejného řádu. Jinak by vzájemný vliv byl buď nepřiměřený, nebo naopak zanedbatelný. Při zadání R0=470 je vcelku jedno, jestli je to chápáno jako 470Ω nebo 470kΩ. Jsou-li ostatní odpory v tomtéž řádu, na zobrazeném grafu se to nijak neprojeví.
Útlum má fyzikální jednotku [dB] zobrazenu, protože tam jiná volba není. Do výpočtu v podobě proměnné GdB vstupuje v této podobě (třeba 20dB), nikoliv jako ve formě čísla udávajícího poměr (tedy 1/10=0.1).
Tak mocná zbraň, jakou je HP-50g, disponuje možností zpracovávat číselné údaje doplněné fyzikálními jednotkami a zapracování této schopnosti do programu by byla ukrutná frajeřina. Znamenalo by to však při zadáních konvenci připojení jednotek striktně dodržovat, a pak je na zvážení, jestli by takové "vylepšení" nebylo ve svém důsledku kontraproduktivní. Jako školní pomůcka budiž, ale pro praktické použití by to asi nebylo. Technici obvykle lnou k jednoduchým věcem...
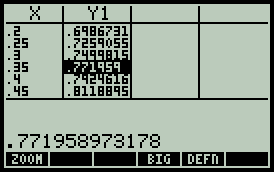
Zobrazené grafy jsou pěkná věc, ale technik by se jistě zajímal o konkrétní hodnoty dělicího poměru v závislosti na míře natočení jezdce potenciometru pro dané zapojení. Po vyprchání fascinace ze zobrazeného průběhu lze přistoupit k průzkumu vypočtených hodnot. Kalkulátor pro takovou činnost nabízí velmi efektivní prostředky, není důvod je nevyužít. — Jako první pokus poslouží stisk kurzorové klávesy LEFT (stejného efektu lze dosáhnout použitím příkazu PICTURE. Zobrazen je obsah systémové proměnné PICT (naposledy sestavený obraz) s obvyklým Soft MENU. Po stisku TRACE (F3) je značka kurzoru svázána s výsledným průběhem (jenom s ním, tečkovaná křivka výchozího neovlivněného průběhu je pouze nakreslená - viz obsah proměnné EQ). (X,Y) (F2) zobrazí hodnoty nezávislé proměnné x (poloha jezdce) a závislá y (dělicí poměr). Pokud by někoho dráždila přítomnost popisků hodnot v grafech, výchozí tečkovaný průběh, nebo osy grafu, může (místo kurzorové klávesy LEFT) současným stiskem L-Shift & 2D/3D vyvolat dialog PLOT SETUP a pokračovat klávesami AXES (F4) (je-li třeba), ERASE (F5) a DRAW (F6). — Druhou možností, jak zjistit číselné údaje, je zobrazení tabulky. Jejího zobrazení je dosaženo současným stiskem L-Shift & TABLE, tedy také vlastními prostředky kalkulátoru.
Opakující se stesky autora těchto textů vyjadřují stále totéž - frustraci z vlastní neschopnosti udržet tématickou linii v intencích RPN. Tendence odbíhat k jiným programovacím jazykům je dlouhodobě neklesající, v případě UserRPL je tato spíše vzestupná. Při vývoji tohoto programu to dlouho vypadalo nadějně alespoň tím, že to bude čistý RPL kód bez algebraických výrazů. Dlouho se zdálo, že argumentem příkazu STEQ v programovém modulu DRAWALL může být « X POS2VAL » resp. « X CALCVAL ». Mohlo to tak být, obrázky by to kreslilo, zpronevěra (ani nic horšího) by se nekonala... Jenže to by pak nešlo používat Some useful PLOT operations for FUNCTION plots, jak se o nich zmiňuje stejnojmenná kapitola HP 50g graphing calculator: user's guide, page 12-5. Ústupek v podobě algebraických výrazů 'POS2VAL(X)' resp. 'CALCVAL(X)' vkládaných do proměnné EQ stojí za to. Dovolí (1) vypočítat plochu pod křivkou průběhu dělicího poměru potenciometru, (2) zakreslit do zobrazeného grafu tangentu pro zadanou polohu jezdce a zveřejnit rovnici této přímky, (3) spočítat funkci derivace k původní funkci 'CALCVAL(X)', (4) určit průsečíky těchto dvou funkcí a určitě many other awesome things, které se změnou průběhu dělicího poměru potenciometru vůbec nijak nesouvisejí, ale kdopak by tomu odolal...
Download | ↑ ↓ |
| Textový tvar | Binární forma | |
|---|---|---|
| Vše naráz | Jednotlivé moduly | |
| potlg.zip | viz seznam zdrojových textů | POTLG.hp |